Symbolic Integration

Thirdly, we have applied our system to a symbolic integration problem as summarised in Table 3. Symbolic Integration involves finding a function which is the integral of the given curve, in this case Cos (X) + 2X + 1. The system is given a set of input and output pairs, and must determine the function that maps one onto the other. The particular function examined was Cos (X) + 2X + 1 with the input values in the range $[0..2\pi]$ and, the target integral curve is Sin(X)+X+X². Similarly to the Symbolic Regression problem described earlier, this problem used the same BNF grammar, including the terminal operators +, *, /,-, Sin, Cos, Exp and Log. The addition, multiplication and Sin operators would have been suffcient to solve this problem but, again to avoid biasing the system other terminal operators were included.

 

Table 3: Grammatical Evolution Tableau for Symbolic Integration

Objective :	Find a function, in symbolic form,
	that is the integral of a curve
	presented either as a mathematical
	expression or as a given finite
	sample of points (xi,yi)
Terminal Operands:	X (the independent variable)
Terminal Operators	The binary operators +, *,
	/,- and the unary operators
	Sin, Cos, Exp and Log
Fitness cases	The given sample of 50 data
	points in the interval [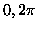$0, 2 \pi$]
Raw Fitness	The sum, taken over the 50 fitness
	cases, of the absolute value of the
	difference between the individual
	genetically produced function
	fj(xi) at the domain point xi
	and the value of the numerical
	integral I(xi)
Standardised Fitness	Same as raw fitness
Hits	The number of fitness cases for
	which the error is less than 0.01
Wrapper	Standard productions to generate
	C functions
Parameters	M = 500, G = 51